片対数グラフと両対数グラフが直線になる理由

グラフの目盛について

片対数グラフはx軸もしくはy軸を対数目盛にしたグラフです。そして、両対数グラフはx軸とy軸の両方を対数目盛にしたグラフです。

対数ではない普通の目盛は線形目盛と呼ばれたりします。普通の目盛（線形目盛）は目盛が1増えたら、同じように目盛で表しているものも1増えます。例えば、物差しの場合、物差しの目盛が1増えたら、1cm増えることになります。2増えたら2cmであり、10増えたら10cmです。
しかし、対数目盛は1増えたら、目盛で表しているものが10倍に増えます。

直線の謎に潜む対数と指数の秘密

対数と指数は同じだと考えることができたりします。繰り返しになりますが、対数で増えるものを対数の目盛に書いているため直線になります。

指数関数と対数関数

下の式について考えます。この式は指数関数と呼ばれます。

\[ y=4^x \]

上の式でxのことを指数といいますが、この指数xは下のように対数の形に変形することができます。

\[ x=\log_4(y) \]

指数と対数は式の書き方が違うだけであって同じ関数です。対数で表された式をみれば、yを対数グラフで書いた場合に直線になる理由がわかると思います。つまり、対数で増えていくyを、同じように対数で増える目盛で書いているから直線になります。

片対数グラフ

指数関数（4のx乗）を片対数グラフに描くと下図のような直線になります。

べき関数と対数関数

下の式について考えます。この式はべき関数と呼ばれます。

\[ y=x^4 \]

対数の形にすると次のようになります。

\[ 4=\log_x(y) \]

xもyも対数の中に組み込まれています。

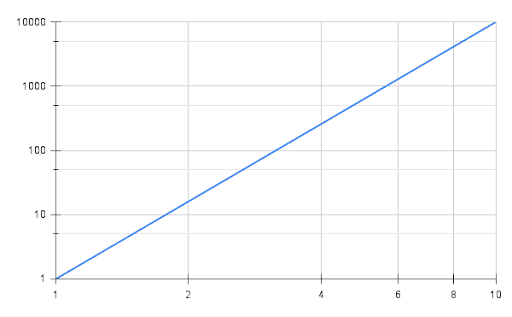
両対数グラフ

べき関数（xの4乗）を両対数グラフに描くと下図のようになります。

指数関数の証明

以下の指数関数について考えます。

\[ y=a^x \]

上の式の両辺に対数を表すlogを作用させます。作用というのは、言い換えるとlog（）の（）の中に入れるという意味です。

\[ \log(y)=\log(a^x) \]

上の式は次のように変形することができます。

\[ \log(y)=x\log(a) \] \[ y=xa=ax \]

指数関数を対数で表すと、式の形が直線の式（y=ax）と同じになります。つまり、指数関数を対数で書くと直線になるということになります。

べき関数の証明

以下のべき関数について考えます。

\[ y=x^a \]

指数関数と同様に、上の式の両辺に対数を表すlogを作用させます。

\[ \log(y)=\log(x^a) \]

上の式は次のように変形することができます。

\[ \log(y)=a\log(x) \] \[ y=ax \]

べき関数を対数で表すと、式の形が直線の式と同じになります。つまり、べき関数を対数で書くと直線になるということになります。